S05E03: The Pulled Groin Extrapolation

An now, the must-watch exciting conclusion of the axion calculation saga on the whiteboards.

Last week we saw two episodes where upon our heroes’ whiteboards unfolded about making an exciting new particle, “the axion” on Earth. Could axions be made inside an artificial Sun made by the National Ignition Facility?  This summer, I was excited about this, but as you already know by now from reading tonight’s whiteboards, I made a terrible, terrible mistake.

To estimate the rate of axions I used the relative power produced by the Sun versus the small compressed sample produced at the National Ignition Facility.  In both cases a material is made so hot that atoms are ripped apart into their constituents: electrons and nuclei.  Such a gas is called a plasma, and plasma is sometimes called “the fourth state of matter” as it is step hotter than just ordinary gas. It is not unfamiliar.  The glowing orange material in a neon sign is a plasma.

The Northern Lights are an example of a plasma you can see. (National Geographic) The last three episode's whiteboards explored if a dense hot plasma could make the elusive Axion particle.

I was comparing the large far-away plasma in the core of the Sun to the tiny, but close, plasma created in the lab.   It initially looked like the laboratory won.  To understand what was wrong,  you first have to understand how the Sun produces its energy.

The strong nuclear interaction likes to bind protons and neutrons together.   And Martha Stewart says, “It’s a good thing”.  Without it, the only atoms we would ever have are hydrogen.  If hydrogen were our only element, we’d have an unperiodic periodic table–with only one entry, hydrogen. In real life, the nucleus of every atom is held together by this force.  And its strength is impressive.  For example, in helium and every element heavier the protons are repelling each other. Same-sign charges (in the protons’ case, both positive) repel with a force increasing as the square of their distance from each other decreases.  A nucleus is extremely small, and those protons are so close they want to fly apart, badly.   The strong interaction overcomes this repulsion and nuclei stay bound.  That’s why it is called the “strong interaction” (or “strong force”).

But there’s a wrinkle.  If you try to bring just two together (either protons or neutrons) there is only one combination that is stable: a pairing of one neutron and one proton.  The pairing of  two protons or two neutrons is not.

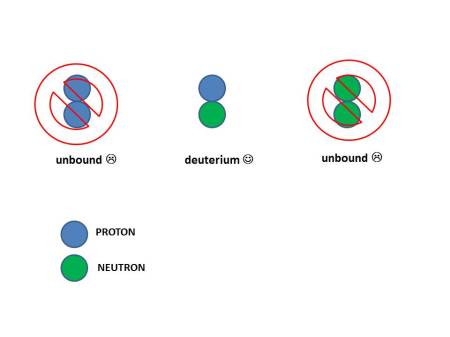
You might think you the strong force could combine any pairing of protons and neutrons. But quantum mechanics only allows a proton and neutron to bind. The result is heavy hydrogen, or "deuterium".

It might seem the reason why two protons are not bound is because of their electric repulsion. But that would not explain why two neutrons are also not bound.  The answer really  lies within the constraints of the quantum mechanics of identical particles.   It turns out that the only way to put two identical neutrons or protons together is if they have angular momentum, but then they are not bound.  We teach our physics majors all about this at UCLA in our introductory quantum mechanics class.  If you can take a quantum mechanics class, I highly recommend it.

The core of the Sun is full of protons but no free neutrons.  So the only way to make energy from them is to convert one of those protons into a neutron so you can bind them.  This bound state of a neutron and proton is still chemically hydrogen, but it has an extra neutron so it is called “heavy hydrogen”, or more technically deuterium.  That’s  the same “heavy” of “heavy water”. “Heavy” water is made with “heavy hydrogen”.   But the reaction does not conserve electric charge so you need a light positively charged particle to fly away, and it turns out to be the anti-matter partner of an electron, which has a positive charge (e⁺), and so is a “positron”.   But that introduces a new problem.  A positron is a type of particle called “lepton” and for reasons not yet understood, you can’t vioate the number of leptons.   So you also need a neutrino (ν)  to be made as well to not create any net leptons. (These neutrinos were detected from the Sun over the last few decades.  They changed our entire understanding of neutrinos but that’s a story for another day.)    It’s easiest to see graphically:

The first step of making energy in the Sun's core by nuclear fusion.

Ultimately these deuteriums (deuteria?) undergo further reactions and the net reaction in the Sun is:

4 protons  –> 1 helium nucleus (2 protons + 2 neutrons)  + 2 neutrinos + lots of energy.

The released energy heats the core and makes the Sun shine. What happened to the positrons?   They are antimatter and as soon as they find an electron (not long at all!) they annihilate into energy.The problem is that first step:  proton +proton -> proton + neutron + positron +neutrino.    To be a bound state we had to convert a proton to a neutron.  The strong interaction cannot do that, but the weak interaction can.   It is a very weak process and that’s why it is called “the weak interaction”.  It is so slow that this dominates the rate of the total fusion in the Sun.

The rate of energy production in the Sun is so slow that pound-for-pound you produce more energy  than the Sun.  Just sitting in front of your computer, digesting your last meal, you produce about 1 Watt of power per kilogram of your body weight.   The sun produces only about 0.0002 Watts per kilogram.   The Sun is just bigger.  A lot bigger. While it is tempting to think of it as a massive nuclear furnace, it really is just smoldering.   We’re lucky too.  If the Sun’s reactions were not throttled by the weak interaction we would be living next to a nuclear bomb, not a star.

But the good people at the National Ignition Facility cannot wait around for such slow reactions.  Instead, they use heavy hydrogen (deuterium). and an even heavier hydrogen with two neutrons and proton, or “tritium”. Their  net reaction is:

deuterium+ tritium -> helium + neutron + energy.

No neutrons or protons changed their identity. They just change who they hang out with.   This proceeds by the strong interactiona nd also releases massive energy.  This reaction is about 10²⁵ times faster than the proton+proton fusion in the Sun. And there’s the rub.  You can’t compare the two Sun’s directly.  The boys’ calculation was off by “only” a factor of 10²⁵.

Before the taping of tonight’s episode, many of the crew members asked me why there was an unhappy face 😦 at the end of one of the whiteboards.  Now you know why.

S05E01 & S05E02: The Skank Reflex Analysis & The Infestation Hypothesis

Some of you may be wondering why two episodes of The Big Bang Theory were broadcast back-to-back tonight. Surely it cannot be a mere coincidence that this is also the first time we have a multi-episode arc on the whiteboards.

Since the beginning of the series, the executive producers have asked me to have Leonard and Sheldon working on solving a real problem on the boards over several episodes. But it wasn’t all that easy. If the boys are working on a known problem with a known solution, then anybody could answer it and spoil the surprise. But if they were working on a known problem with no known solution, there are already hundreds if not thousands of minds working on it, and how could they (meaning I) solve it by season’s end?

Axions: exciting new elementary particles, or a detergent?

We needed a fresh, tractable, problem. And over the summer I had an idea. The idea would allow physicists to make a never-before seen particle. And it could solve the dark matter problem. Perhaps our galaxy is filled with these particles. They would provide the gravitational glue that keeps the galaxy rapidly spinning, but have so weakly interacting they would usually pass through the entire Earth undetected. I thought I found a new way of making a particle that was hypothesized over three decades ago,  “The Axion”.

The Axions’ role in solving the dark matter problem is actually just a nice side effect. These particles were originally conceived in the late 1970’s to give a natural explanation of why the strong nuclear force (a.k.a., quantum chromodynamics) obeys certain symmetries so well-too well. It is a happy accident that axions could also account for all the dark matter in the galaxy. It solves two important unrelated problems at once and if elegance were a guide then theorists would likely consider the matter settled.

But physics is an experimental science and sheer elegance is not enough. The history of physics is filled with ideas that were simple, elegant, and wrong.   Physics is an experimental science and we have to find their signature experimentally.

In very dense environments at high temperature, charged particles will start to radiate axions efficiently. The core of the Sun is over 13 million kelvins (over 23 millions degrees Farenheit) and is 150 times the density of water. As shown on the whiteboards’ Feynman diagrams, electrons in this enviroment could produce a detectable number of axions. Because they are so weak they penetrate the entire Sun, leaving in all directions. A rare few strike the Earth.

So all astrophysicists have to do is find them leaving the Sun. CERN is not only home to the Large Hadron Collider, but also a clever telescope that points at the Sun. But this is no ordinary telescope.  Physicists need not only to detect these weakly interacting axions efficiently enough to find a signal, but in a way that cannot be mimicked by more mundane processes, called backgrounds. One of the funny behaviors of axions is that inside a strong, uniform magnetic field they will convert into light. Specificially, one axion will convert to one single particle of light, a photon. Because the axions are made in the heat of the core of the Sun they have an energy corresponding to 13 million kelvins. So each photon from a converted axion from the Sun will actually be an energetic X-ray.

Every morning and every evening, astrophysicists at CERN, took a prototype magnet borrowed from the Large Hadron Collider project and pointed it at the Sun. They called their device CAST, the CERN Axion Solar Telescope. If they ever see X-rays emerging from the magnetic field that would be a tell-tale sign of axions. They can check they weren’t seeing local radioactive backgrounds by pointing the telescope away from the Sun. Unfortunately to date they have seen none.

Not Galileo's optics: the CERN Axion Solar Telescope (CAST) is actually a large magnet pointed at the Sun.

Zillions of axions are wasted in this technique. The Sun would be pouring out axions in all directions, but only those entering the tiny front aperture of the magnet are detectable. That’s an efficiency of about 1 in 10²⁵ axions. And even only a tiny fraction of these would be converted.

This summer I wondered if we could do better. The main problem is the Earth is so far from the Sun. Meanwhile physicists at Lawrence Livermore National Laboratory in California are making an artificial Sun in the laboratory. They aim 192 lasers at a small pellet of heavy water and for a short time they achieve the density and temperatures of the Sun.  Exceed it, even. But not just short, but a very short time, about a hundred billionths of a second. They do this amazing feat to copy the fusion power of the Sun, as a clean almost limitless source of energy for us on earth. It is called fusion because the core of Sun converts protons into heavier elements, mostly helium. The particles are fused together into this heavier atomic nucleus, and so is called fusion.    Because the resulting nucleus is less massive than the sum of the original protons, by Einstein’s famous formula E=mc², the missing mass is converted to enormous amounts of energy.

When the process is successful, we can think of “burning” hydrogen into helium to release energy, in analogy with how a burning of a log releases energy as heat. The major difference is rather than a chemical reaction which drives fire, this is a nuclear reaction. Nuclear reactions typically release a million times more energy than chemical reactions for a given supply of fuel. The physicists at Lawrence Livermore call the successful implosions “ignition” and built the National Ignition Facility with its 192 powerful lasers to do it.

The National Ignition Facility focuses 192 lasers onto a small pellet, briefly creating an artificial Sun on Earth.

The National Ignition Facility is the prototype for what its physicists think will be a power plant as powerful as the big coal plants or nuclear power plants.  Even a 1000 gigawatt plant is still a lot less power than the Sun’s 10¹⁷ gigawatts, but we can put the magnet much closer:  We could put an axion telescope 10 meters away instead of 150 billion meters away, our distance from the Earth. Since the rate improves as the square of the distance drops, that is a whopping improvement of 10²⁰, more than making up for the lower power.

The numbers looked really good. I was excited. Accounting for distance and power, I reckoned I could do about 1000 times better than the CERN Axion Solar Telescope. That didn’t even account for the fact that the background would be lower since the artificial Sun is only on for 100 billionths of a second, not all day. And since the magnets don’t have to follow the Sun in the sky we could make them much larger. The emission mechanism even looked more efficient than the Sun.

But that’s not the whole story. This was actually a three-episode whiteboard arc. I suppose CBS wanted to create some suspense and the third episode will not be aired until next week. That next episode contains the result of my summer’s worth of calculations. If you think you know the answer, comment below. Otherwise, tune in next week to find out if we are on the verge of creating and detecting axions on Earth.

To be continued…